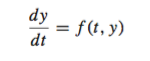Posts

Showing posts from June, 2016

Computer History Museum - A visit

Image
As a child, I used to imagine that when I grow up I will work in a bookstore. I will sell books and in spare time read all the books. Whenever I get a chance to visit a big bookstore or Library, I feel as If I have entered heaven, my spine is thrilled with electric spikes.
This August, I got a chance to visit San Jose (Was there to attend an international conference ASONAM 2016 in San Francisco). Feeling a bit adventurous I tried Airbnb for the first time and stayed with Venna, a very sweet lady. When we reached, she suggested that since I am into computers I should visit Computer History Museum, I accepted her suggestion and am very happy that I did. The museum kindled the child in me, and once again I was back to childhood (not that I have really grown old), seeing the Babbage difference engine, the PDP-1, the Jacquard loom, I was transcended into a new world. The museum showcased the history of computers bringing them back to life through their gigantic exhibits. The exhibition Rev…
Post a Comment
Read more

Solving Differential Equations:One step Methods

Image
A lot of problems in science and engineering involve solving differential equations pendulums, RLC circuits, diffusion and so on. An ordinary differential equation can be expressed as:  Generally solution of this equation is of the form:

Here 'phi' is the increment function or slope and h is the step size.  Thus, an estimate of slope is used to extrapolate the new value y(i+1) when the previous value y(i) is known, over a distance h.  The methods which are based on above equation are called one step methods. They all only differ by the definition of increment function.
Solved Example: Calculate y(2) for in the interval t=[0,2]. Given y(0)=1, for

Solution: Consider h=1, here Using Euler Method:

Post a Comment
Read more

Separate Axis Theorem

Image
IntroductionSeparate Axis Theorem (SAT) is a method to determine whether two convex shapes are intersecting or not. The theorem states that, “Given two convex shapes there exists a line onto which their projections will be separate if and only if they are not intersecting”. It is the most commonly used method for collision detection.SAT also returns the minimum penetration vector, or minimum translation vector, the shortest distance that the colliding object can be moved in order to no longer be colliding.
The basic idea is imagine you have two convex shapes, let us consider two triangles as given in fig 1. We shine light on them from different angles and observe shadows on the wall perpendicular to the direction of light, if doing this work around the shapes we do not find a gap in the shadows, then the objects are colliding. But, if we are able find a gap, then they are not intersecting/colliding.
Post a Comment
Read more

RAM : Different Speeds Different Sizes

Image
Have you ever needed to replace the RAM of your desktop or Laptop? Have you wondered what if you add two RAM off different speeds, say one at 1600 Mhz and other 1330 MHz? Or if you mixed the sizes one RAM of 8GB and another of 2GB?

The worst case scenario, system may not boot!! The system may not be able to come to the optimized value of speed or size.

The best scenario, system optimize the speed to the lowest configuration (actually it is more like two resistances in parallel, the resultant is lowest than the two). Shown below is Memory configuration of Mac Mini, when two 8GB DDR3 RAMs one of 1600MHz (Crucial) and other of 1330 MHz (Corsair) is put, see the net speed 1067Mhz, lower than the lowest.


Exactly similar thing will happen if the two memories are different. You will not get the net result of 10GB memory (8+2), because OS treats the two equal, while paging, hence even though it will show 8GB + 2GB but the memory used will be <4GB.

Verdict:Do not mix RAM sizes or speeds. RAM is…
Post a Comment
Read more